| Home | Curatorial Essays | Phil Huneke |
Phil Huneke-- in "Drawing on Sculpture" Bertha Urdang Gallery, 1979.p. 15.. Catalogue. |
|||||||||||||||||||||||||||||||
| "Smooth Tesselations of a Sphere and Other Surfaces" | |||||||||||||||||||||||||||||||
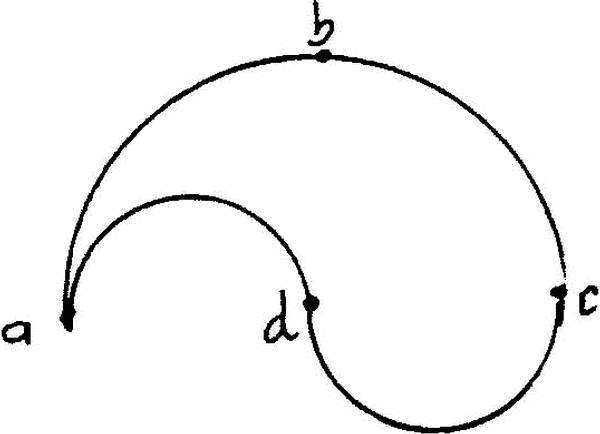
Derivation The 2-sphere is smoothly tesselated by two copies of a circular disc D Mathematical definitions for a smooth tesselation of a surface by copies of a disc Dn
Hence the parameters n and p give the topological type of the surface of any such real world sculpture.
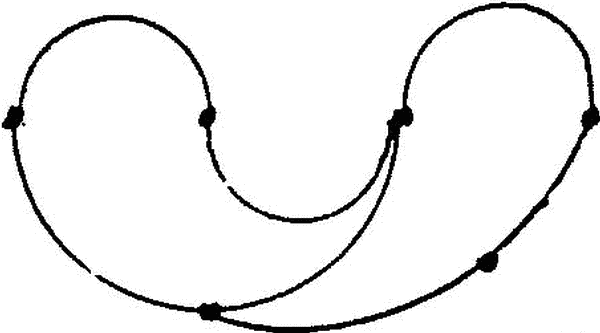
Schematization Betty Collings indicated all similar sculptures by using a circular scheme to display her Con(jug)ate series of sculptures. Any sculpture in this sereies can be continuously deformed into another so that each intermediate stage of the deformation gives an example of a smooth tesselation by two copies of D0. Mathematically, the set X0,2, of all smooth tesselations formed with two copies of D0 canonically corresponds to the set of all isometries of a circle, or equivalently, to the topological groupd of all real orthogonal 2x2 matrices. Hence X0,2 is two disjoint circles, each tessellation representing a position on a circle. The Con(jug)ation sculptures of Collings are thus naturally arranged on X0,2. In general, the set Xn,p of all smooth tesselations of a surface M with p copies of a fixed disc Dn As the parameters n and p increase, so do the degrees of freedom for the continuous deformations and hence also the complexity of the schema Xn,p. However, the spaces Xn,p seem to have geometrical descriptions as CW-complexes. The component of X1,4 cataloguing all smooth tesselations of the 2-sphere with four copies of D1, all with the same orientation, has a two point compactification wihich is homeomorphic to Zeeman's Dunce cap (a contractable but not collapsable 2-complex) with a disc attached at its circular 1-skeleton. Twelve of Betty Collings' sculptures in the Anolatabulata series are represented as positions in this space, the others in this series sbelong in other analogous components of X1,4. Phil Huneke. Professor of Mathematics, Ohio State University. |
|||||||||||||||||||||||||||||||
Click on images to enlarge.
| Home | Curatorial Essays | Phil Huneke |